对称性在积分中的应用
对称性在积分中的应用
杨子容
湖北第二师范学院 湖北武汉 430000
摘要:积分计算是数学计算中一个非常重要的内容,对于复杂的积分计算问题,运用常见的解题方法已无法解决,而如果巧妙地利用对称性就可以缩减计算量。下面深入研究了二重积分、第一型曲线积分中当积分区域关于坐标轴、坐标面对称且被积函数有奇偶性时的几种积分计算公式,并列举实例说明。
http://www.baixinglunwen.com/
关键词:对称性 奇偶性 坐标轴 积分 坐标面
1. 对称性在二重积分中的应用
定理1[1-2]:设函数![]() 在有界闭区域
在有界闭区域![]() 上连续,若
上连续,若![]() 关于
关于![]() 轴对称,其中
轴对称,其中![]() ,则有
,则有
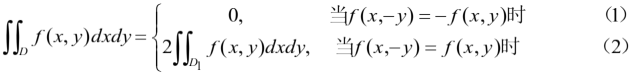
若![]() 关于
关于![]() 轴对称时有类似结论.
轴对称时有类似结论.
例1:计算![]() ,其中
,其中![]() 是由直线
是由直线![]() ,
,![]() 和
和![]() 所围成.
所围成.
解:原式=![]() ,由于
,由于![]() 关于
关于![]() 轴对称,记
轴对称,记![]() ,令
,令![]() ,
,![]() .
.
因为![]() ,故由公式(1)可得
,故由公式(1)可得![]() ,
,
而![]() ,故由公式(2)可得
,故由公式(2)可得![]() ,
,
所以![]() .
.
除此之外,对于积分变量可以交换顺序的题目,根据具体的情况能够将各个变量前的系数化为一样以至达到简便过程的效果,对于不能直接使用的题目,也可以通过变换创造轮换对称性[3-4]。
2. 对称性在第一型曲线积分中的应用
曲线积分研究的是定义在二维或三维曲线段上函数的积分[5]。
定理2:设函数![]() 在平面曲线
在平面曲线![]() 上连续,那么若
上连续,那么若![]() 关于
关于![]() 轴对称,
轴对称,![]() ,则
,则
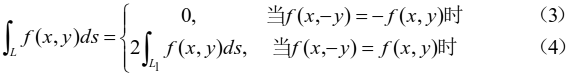
证明:设![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称,记
轴对称,记![]() 为
为![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,其中
,其中![]() ,所以
,所以
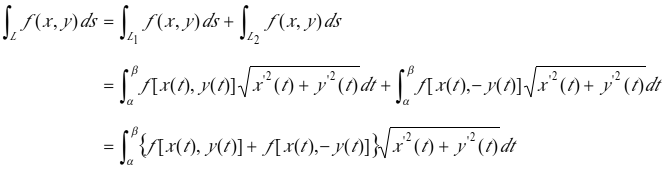
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
若![]() 关于
关于![]() 轴对称时也有类似结论.
轴对称时也有类似结论.
例2:计算![]() ,其中
,其中![]() 是以原点为中心,
是以原点为中心,![]() 为半径的右半圆周.
为半径的右半圆周.
解:原式=![]() ,由于
,由于![]() 关于
关于![]() 轴对称,记
轴对称,记![]() ,令
,令![]() ,
,![]() .因为
.因为![]() ,故由公式(3)可得
,故由公式(3)可得![]() ,而
,而![]() ,故由公式(4)可得
,故由公式(4)可得![]() ,所以
,所以![]() .
.
定理3:设函数![]() 在空间光滑(或分段光滑)的曲线
在空间光滑(或分段光滑)的曲线![]() 上连续,那么若
上连续,那么若![]() 关于
关于![]() 面对称,其中
面对称,其中![]() ,则有
,则有
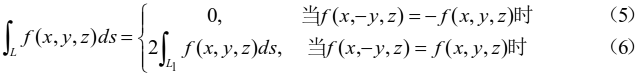
证明:设![]() ,且
,且![]() 与
与![]() 关于
关于![]() 面对称,记
面对称,记![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,所以
,所以
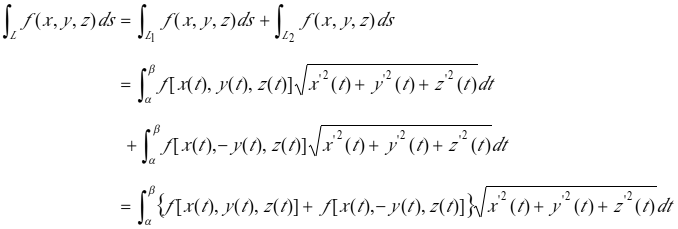
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
若![]() 关于
关于![]() 、
、![]() 面对称时也类似结论.
面对称时也类似结论.
3. 小结
本文研究了对于二重积分、第一型曲线积分,若积分区域是关于某个坐标轴对称或关于某个坐标面对称,当被积函数具有奇偶性时,则其积分值遵循偶倍奇零的性质。
参考文献
[1]薛春荣,王芳.对称性在定积分及二重积分计算中的应用[J].科学技术与工程,2010,10(1):172-175.
[2]赵金兰.积分区域对称性在计算二重积分中的应用[J].山西煤炭管理干部学院学报,2015,28(3):157-158.
[3]朱玉.重积分计算中对称性的应用[J].高等数学研究,2019,22(2):17-18,21.
[4]徐立峰.对称性在重积分计算中的应用[J].高等数学研究,2013,16(2):37-39.
[5]华东师范大学数学系.数学分析(第四版)[M].北京:高等教育出版社,2010















